今回は階層型ニューラルネットワークの基本となる多層パーセプトロンをDeepLearning 4jで構築する方法について見ていく。
■ 多層パーセプトロンとは?
多層パーセプトロンはニューロンを階層状にならべた階層型ニューラルネットワークの基本となっている。多層パーセプトロンは中間層がすべて全結合層(前層の全ニューロンと接続する層)で構成されたニューラルネットワークであり、非線形な関数を近似することができる。多層パーセプトロンの構成は以下のようなイメージとなる。
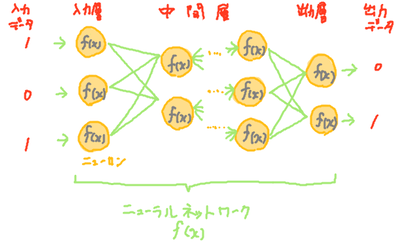
図:多層パーセプトロンのイメージ
表:多層パーセプトロンで利用する層の種類
| 層の名称 |
Deeplearning4j内のクラス |
内容 |
全結合層
(略:FC,RELU) |
DenseLayer |
前層のニューロンに対し全結合を行う。 |
出力層
(略:OUTPUT) |
OutputLayer |
全結合層と同様の構造を持つ。DeepLearing4jでニューラルネットワークを構成する場合、必ず含めないといけない層。 |
多層パーセプトロンの特徴は非線形関数を近似できるため画像認識などの高度な処理も行える点にある。しかし、ニューロン数が多くなるに従い計算量が膨大な数になってしまうという欠点があるため、多層パーセプトロンがそのまま実用される場合は少ない。ただし、他のニューラルネットワーク内で利用されたり、階層型ニューラルネットワークの基本的な挙動を確認するため、理解しておいたほうがよいニューラルネットワークである。
全結合層
全結合層内の\(i\)番目のニューロンは以下の図のような動作を行う。すなわち、前層の\(j\)番目のニューロン出力\(x_j\)に対して別々の重み\(v_{ij}\)を乗じたものの総和をとり(ネット値)、その総和から閾値\(\theta\)(バイアスとも呼ぶ)を引いた値を活性化関数と呼ばれる関数\(f(x)\)で処理した結果を出力値\(h_i\)としている。
学習フェーズで重み\(v_{ij}\)と閾値\(\theta\)を変更することにより、任意の式の近似式を得ることができる。

\begin{align}
h_i & = f( \sum_{k=0}^n v_{ik}x_k - \theta ) \\
& = f( v_{i1}x_1 + v_{i2}x_2 + \cdots + v_{in}x_n - \theta )
\end{align} |
|
| 変数 |
内容 |
| \(n\) |
入力値の個数。各層毎に異なる |
| \(x_i\) |
i番目の入力値(教師データ) |
| \(v_{ij}\) |
各層内のi番目ニューロンで、入力jにかける加重パラメータ(結合荷重) |
|
| \(h_i\) |
中間層のi番目ニューロンの出力値。(次の層の入力値にもなる) |
| \(f(x)\) |
活性化関数(シグモイド関数が一般的に利用される)
\begin{align}
f(x) & = \frac{1}{1+e^{-x}}
\end{align} |
| \(\theta\) |
閾値 |
図:多層パーセプトロンを構成するニューロンの数式
■ サンプルプログラム
以下にDeepLearning4jで多層パーセプトロンを構成するサンプルプログラムを示す。サンプルではXOR計算を行う3層の多層パーセプトロンを構成し、4つの学習データを用いて2000回の学習(誤差逆伝搬法)を行っている。活性化関数はシグモイド関数を、誤差関数は誤差の平方和(\(\sum (t_i - o_i)^2\))を利用している。
◇サンプルプログラム
import org.deeplearning4j.nn.api.OptimizationAlgorithm;
import org.deeplearning4j.nn.conf.MultiLayerConfiguration;
import org.deeplearning4j.nn.conf.NeuralNetConfiguration;
import org.deeplearning4j.nn.conf.Updater;
import org.deeplearning4j.nn.conf.layers.DenseLayer;
import org.deeplearning4j.nn.conf.layers.OutputLayer;
import org.deeplearning4j.nn.multilayer.MultiLayerNetwork;
import org.deeplearning4j.nn.weights.WeightInit;
import org.deeplearning4j.optimize.listeners.ScoreIterationListener;
import org.nd4j.linalg.api.ndarray.INDArray;
import org.nd4j.linalg.dataset.DataSet;
import org.nd4j.linalg.factory.Nd4j;
import org.nd4j.linalg.lossfunctions.LossFunctions;
/**
* XOR計算を行う多層パーセプトロン
* @author karura
*/
public class MultiPerceptron
{
// メイン関数
public static void main(String[] args) throws Exception
{
// 変数定義
int seed = 123; // 乱数シード
int iterations = 2000; // 学習の試行回数
int inputNum = 2; // 入力数
int middleNum = 10; // 隠れ層のニューロン数
int outputNum = 1; // 出力数
INDArray tIn = Nd4j.create( new float[]{ 1 , 1 , // 入力1
1 , 0 , // 入力2
0 , 1 , // 入力3
0 , 0 }, // 入力4
new int[]{ 4 , 2 } ); // サイズ
INDArray tOut = Nd4j.create( new float[]{ 0 , 1 , 1 , 0} , // 出力1~4
new int[]{ 4 , 1 } ); // サイズ
DataSet train = new DataSet( tIn , tOut ); // 入出力を対応付けたデータセット
System.out.println( train );
// ニューラルネットワークを定義
MultiLayerConfiguration.Builder builder = new NeuralNetConfiguration.Builder()
.seed(seed)
.iterations(iterations)
.learningRate(0.01)
.weightInit(WeightInit.SIZE)
.optimizationAlgo(OptimizationAlgorithm.STOCHASTIC_GRADIENT_DESCENT)
.updater( Updater.NONE )
.list()
.layer(0, new DenseLayer.Builder()
.nIn(inputNum)
.nOut(middleNum)
.activation("sigmoid").build())
.layer(1, new OutputLayer.Builder( LossFunctions.LossFunction.MSE )
.nIn(middleNum)
.nOut(outputNum)
.activation("sigmoid")
.build())
.backprop(true).pretrain(false);
// ニューラルネットワークを作成
MultiLayerConfiguration conf = builder.build();
MultiLayerNetwork perceptron = new MultiLayerNetwork(conf);
perceptron.init();
// 確認用のリスナーを追加
perceptron.setListeners( new ScoreIterationListener(1) );
// 学習(fit)
perceptron.fit( train );
// パーセプトロンの使用
for( int i=0 ; i<train.numExamples() ; i++ )
{
// i個目のサンプルについて、
INDArray input = train.get(i).getFeatureMatrix();
INDArray answer = train.get(i).getLabels();
INDArray output = perceptron.output( input , false );
System.out.println( "result" + i );
System.out.println( " input : " + input );
System.out.println( " output : " + output );
System.out.println( " answer : " + answer );
System.out.flush();
}
}
}
◇実行結果
20:43:12.444 [main] DEBUG org.nd4j.nativeblas.NativeOps - Number of threads used for linear algebra 32
20:43:12.476 [main] WARN org.nd4j.jita.conf.CudaEnvironment - Please note, CudaEnvironment is already initialized. Configuration changes won't have effect
…中略…
===========INPUT===================
[[1.00, 1.00],
[1.00, 0.00],
[0.00, 1.00],
[0.00, 0.00]]
=================OUTPUT==================
[0.00, 1.00, 1.00, 0.00]
…中略…
20:43:41.441 [main] INFO o.d.o.l.ScoreIterationListener - Score at iteration 1999 is 0.0024183732457458973
result0
input : [1.00, 1.00]
output : 0.09
answer : 0.00
result1
input : [1.00, 0.00]
output : 0.93
answer : 1.00
result2
input : [0.00, 1.00]
output : 0.92
answer : 1.00
result3
input : [0.00, 0.00]
output : 0.04
answer : 0.00
◇解説
学習用データの準備は30行目~38行目で行っており、XORの計算の入力と出力値を作成している。1つ目の学習データを見てみると入力(1,1)に対して、出力0を設定している。標準出力を見てみると、入力のi番目データをXORした結果を出力のi番目データとなっていることが確認できる。
多層パーセプトロンの構成は40行目~63行目で行っている。注意点としては重みの初期化に定数「WeightInit.Size」を指定していることであり、他の初期化方法では学習がうまくいかない。これはシグモイド関数を利用していることに起因すると思われる。シグモイド関数ではある範囲の入力値(例えば-2<x<2)を0~1の値に変換するが、この範囲外(例えばx<-2,2<x)の値は常に0か1になってしまう。このため範囲外では勾配値が常に0となり、勾配を利用した学習方法はうまく機能しないという特性がある。WeightInit.Sizeの場合にのみうまく学習できるのは、シグモイド関数で学習可能な入力値となるように、重みが初期化されるためと考えられる。実際、WeightInit.Size以外の初期化方法では値が-1~1程度の値に初期化されるが、WeightInit.Sizeでは0~2(入力配列の長さ)に初期化されることはデバッグすれば確認できる。
学習は69行目で行い、学習後の多層パーセプトロンの利用は72行目~84行目で行っている。多層パーセプトロンの利用では学習用のデータを転用しており、i番目の入力データを取得し(getFreatureMatrix関数)、その出力値とi番目データの正解値(getLabels関数)を標準出力に出力している。結果としては、すべてのXOR計算において誤差が0.1以下に収まっていることが確認できる。
■ 参照
- ニューラルネットワーク入門
